Category theory

We have seen how a founding pillar of functional programming is composition.

And how do we solve problems? We decompose bigger problems into smaller problems. If the smaller problems are still too big, we decompose them further, and so on. Finally, we write code that solves all the small problems. And then comes the essence of programming: we compose those pieces of code to create solutions to larger problems. Decomposition wouldn't make sense if we weren't able to put the pieces back together. - Bartosz Milewski

But what does it means exactly? How can we state whether two things compose? And how can we say if two things compose well?

Entities are composable if we can easily and generally combine their behaviours in some way without having to modify the entities being combined. I think of composability as being the key ingredient necessary for achieving reuse, and for achieving a combinatorial expansion of what is succinctly expressible in a programming model. - Paul Chiusano

We've briefly mentioned how a program written in functional styles tends to resemble a pipeline:

const program = pipe(
  input,
  f1, // pure function
  f2, // pure function
  f3, // pure function
  ...
)

But how simple it is to code in such a style? Let's try:

import { pipe } from 'fp-ts/function'
import * as RA from 'fp-ts/ReadonlyArray'

const double = (n: number): number => n * 2

/**
 * Given a ReadonlyArray<number> the program doubles the first element and returns it
 */
const program = (input: ReadonlyArray<number>): number =>
  pipe(
    input,
    RA.head, // compilation error! Type 'Option<number>' is not assignable to type 'number'
    double
  )

Why do I get a compilation error? Because head and double do not compose.

head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number

head's codomain is not included in double's domain.

Looks like our goal to program using pure functions is over..Or is it?

We need to be able to refer to some rigorous theory, one able to answer such fundamental questions.

We need to refer to a formal definition of composability.

Luckily, for the last 70 years ago, a large number of researchers, members of the oldest and largest humanity's open source project (mathematics) occupied itself with developing a theory dedicated to composability: category theory, a branch of mathematics founded by Saunders Mac Lane along Samuel Eilenberg (1945).

Categories capture the essence of composition.

Saunders Mac Lane

(Saunders Mac Lane)

(Samuel Eilenberg)

We'll see in the following chapters how a category can form the basis for:

• a model for a generic programming language
• a model for the concept of composition

Definition

The definition of a category, even though it isn't really complex, is a bit long, thus I'll split it in two parts:

• the first is merely technical (we need to define its constituents)
• the second one will be more relevant to what we care for: a notion of composition

Part I (Constituents)

A category is a pair of (Objects, Morphisms) where:

• Objects is a collection of objects
• Morphisms is a collection of morphisms (also called "arrows") between objects

Note. The term "object" has nothing to do with the concept of "objects" in programming. Just think about those "objects" as black boxes we can't inspect, or simple placeholders useful to define the various morphisms.

Every morphism f owns a source object A and a target object B.

In every morphism, both A and B are members of Objects. We write f: A ⟼ B and we say that "f is a morphism from A to B".

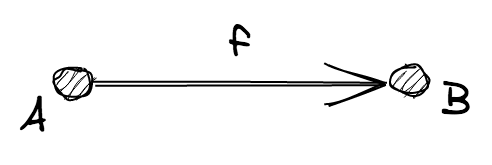
Note. For simplicity, from now on, I'll use labels only for objects, skipping the circles.

Part II (Composition)

There is an operation, ∘, called "composition", such as the following properties hold true:

• (composition of morphisms) every time we have two morphisms f: A ⟼ B and g: B ⟼ C in Morphisms then there has to be a third morphism g ∘ f: A ⟼ C in Morphisms which is the composition of f and g

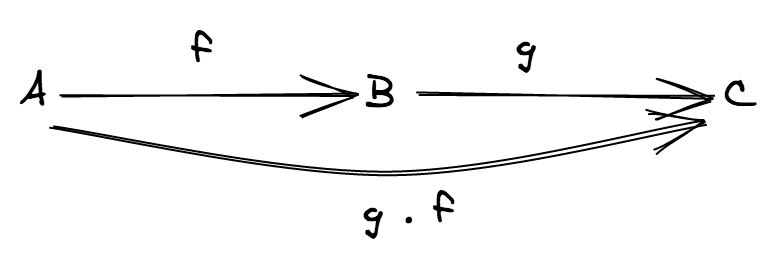
• (associativity) if f: A ⟼ B, g: B ⟼ C and h: C ⟼ D then h ∘ (g ∘ f) = (h ∘ g) ∘ f

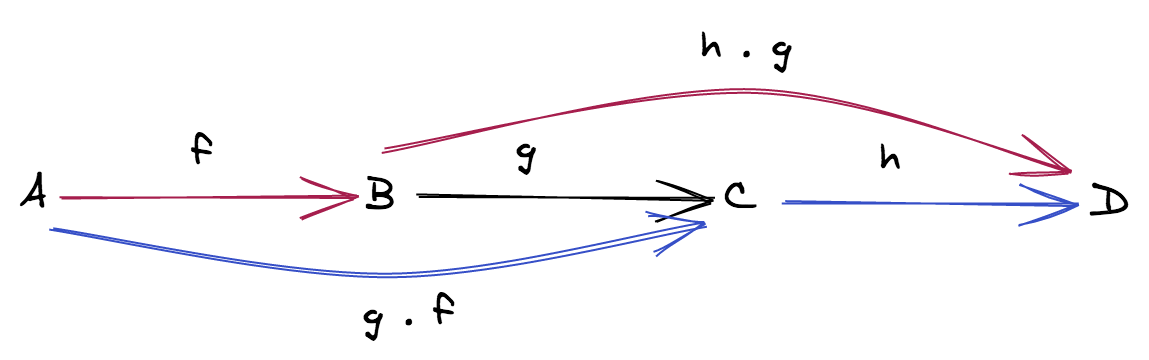
• (identity) for every object X, there is a morphism identity: X ⟼ X called identity morphism of X, such as for every morphism f: A ⟼ X and g: X ⟼ B, the following equation holds true identity ∘ f = f and g ∘ identity = g.

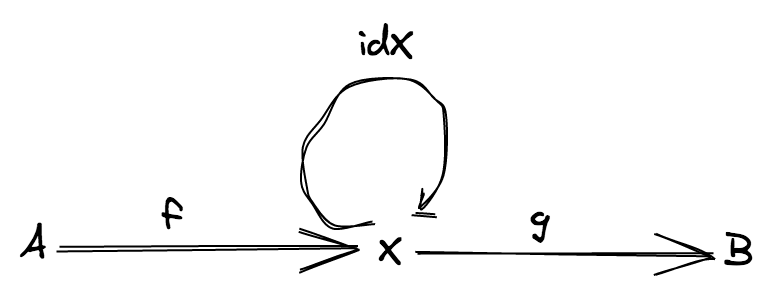
Example

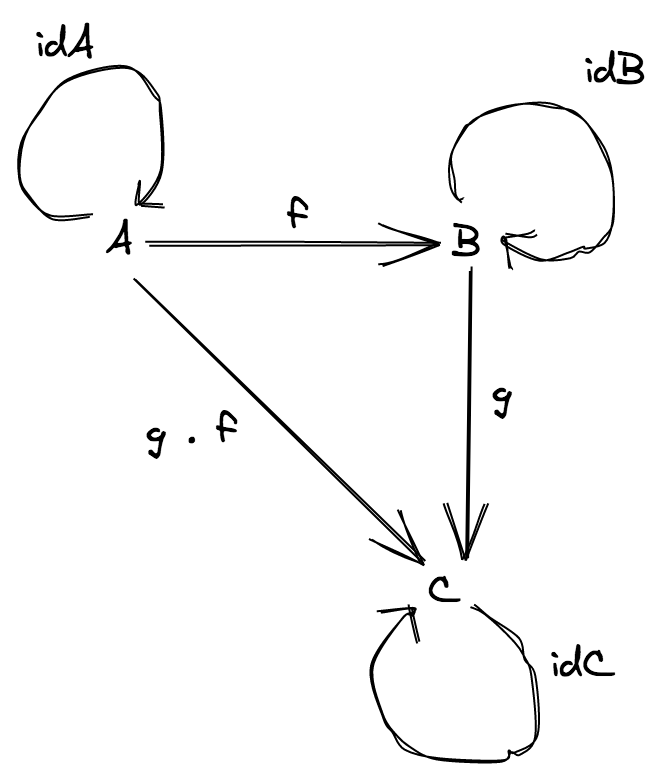
This category is very simple, there are three objects and six morphisms (1_A, 1_B, 1_C are the identity morphisms for A, B, C).

Modeling programming languages with categories

A category can be seen as a simplified model for a typed programming language, where:

• objects are types
• morphisms are functions
• ∘ is the usual function composition

The following diagram:

can be seen as an imaginary (and simple) programming language with just three types and six functions

Example given:

• A = string
• B = number
• C = boolean
• f = string => number
• g = number => boolean
• g ∘ f = string => boolean

The implementation could be something like:

const idA = (s: string): string => s

const idB = (n: number): number => n

const idC = (b: boolean): boolean => b

const f = (s: string): number => s.length

const g = (n: number): boolean => n > 2

// gf = g ∘ f
const gf = (s: string): boolean => g(f(s))

A category for TypeScript

We can define a category, let's call it TS, as a simplified model of the TypeScript language, where:

• objects are all the possible TypeScript types: string, number, ReadonlyArray<string>, etc...
• morphisms are all TypeScript functions: (a: A) => B, (b: B) => C, ... where A, B, C, ... are TypeScript types
• the identity morphisms are all encoded in a single polymorphic function const identity = <A>(a: A): A => a
• morphism's composition is the usual function composition (which we know to be associative)

As a model of TypeScript, the TS category may seem a bit limited: no loops, no ifs, there's almost nothing... that being said that simplified model is rich enough to help us reach our goal: to reason about a well-defined notion of composition.

Composition's core problem

In the TS category we can compose two generic functions f: (a: A) => B and g: (c: C) => D as long as C = B

function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
  return (a) => g(f(a))
}

function pipe<A, B, C>(a: A, f: (a: A) => B, g: (b: B) => C): C {
  return flow(f, g)(a)
}

But what happens if B != C? How can we compose two such functions? Should we give up?

In the next section we'll see under which conditions such a composition is possible.

Spoiler

• to compose f: (a: A) => B with g: (b: B) => C we use our usual function composition
• to compose f: (a: A) => F<B> with g: (b: B) => C we need a functor instance for F
• to compose f: (a: A) => F<B> with g: (b: B, c: C) => D we need an applicative functor instance for F
• to compose f: (a: A) => F<B> with g: (b: B) => F<C> we need a monad instance for F

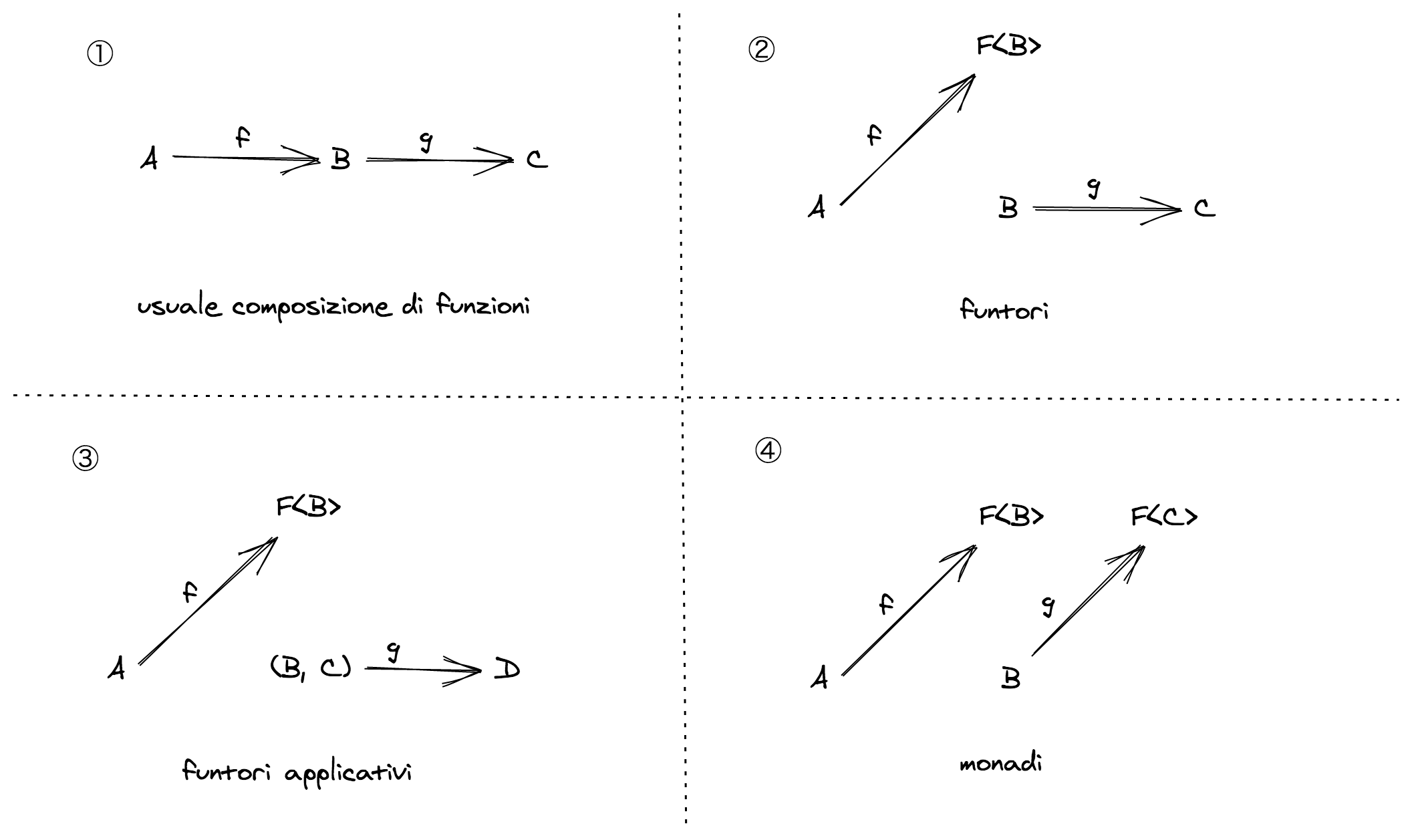
The problem we started with at the beginning of this chapter corresponds to the second situation, where F is the Option type:

// A = ReadonlyArray<number>, B = number, F = Option
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number

To solve it, the next chapter will talk about functors.