Modeling composition through Monoids

Let's recap what we have seen till now.

We have seen how an algebra is a combination of:

• some type A
• some operations involving the type A
• some laws and properties for that combination.

The first algebra we have seen has been the magma, an algebra defined on some type A equipped with one operation called concat. There were no laws involved in Magma<A> the only requirement we had was that the concat operation had to be closed on A meaning that the result:

concat(first: A, second: A) => A

has still to be an element of the A type.

Later on we have seen how adding one simple requirement, associativity, allowed some Magma<A> to be further refined as a Semigroup<A>, and how associativity captures the possibility of computations to be parallelized.

Now we're going to add another condition on Semigroup.

Given a Semigroup defined on some set A with some concat operation, if there is some element in A – we'll call this element empty – such as for every element a in A the two following equations hold true:

• Right identity: concat(a, empty) = a
• Left identity: concat(empty, a) = a

then the Semigroup is also a Monoid.

Note: We'll call the empty element unit for the rest of this section. There's other synonyms in literature, some of the most common ones are neutral element and identity element.

We have seen how in TypeScript Magmas and Semigroups, can be modeled with interfaces, so it should not come as a surprise that the very same can be done for Monoids.

import { Semigroup } from 'fp-ts/Semigroup'

interface Monoid<A> extends Semigroup<A> {
  readonly empty: A
}

Many of the semigroups we have seen in the previous sections can be extended to become Monoids. All we need to find is some element of type A for which the Right and Left identities hold true.

import { Monoid } from 'fp-ts/Monoid'

/** number `Monoid` under addition */
const MonoidSum: Monoid<number> = {
  concat: (first, second) => first + second,
  empty: 0
}

/** number `Monoid` under multiplication */
const MonoidProduct: Monoid<number> = {
  concat: (first, second) => first * second,
  empty: 1
}

const MonoidString: Monoid<string> = {
  concat: (first, second) => first + second,
  empty: ''
}

/** boolean monoid under conjunction */
const MonoidAll: Monoid<boolean> = {
  concat: (first, second) => first && second,
  empty: true
}

/** boolean monoid under disjunction */
const MonoidAny: Monoid<boolean> = {
  concat: (first, second) => first || second,
  empty: false
}

Quiz. In the semigroup section we have seen how the type ReadonlyArray<string> admits a Semigroup instance:

import { Semigroup } from 'fp-ts/Semigroup'

const Semigroup: Semigroup<ReadonlyArray<string>> = {
  concat: (first, second) => first.concat(second)
}

Can you find the unit for this semigroup? If so, can we generalize the result not just for ReadonlyArray<string> but ReadonlyArray<A> as well?

Quiz (more complex). Prove that given a monoid, there can only be one unit.

The consequence of the previous proof is that there can be only one unit per monoid, once we find one we can stop searching.

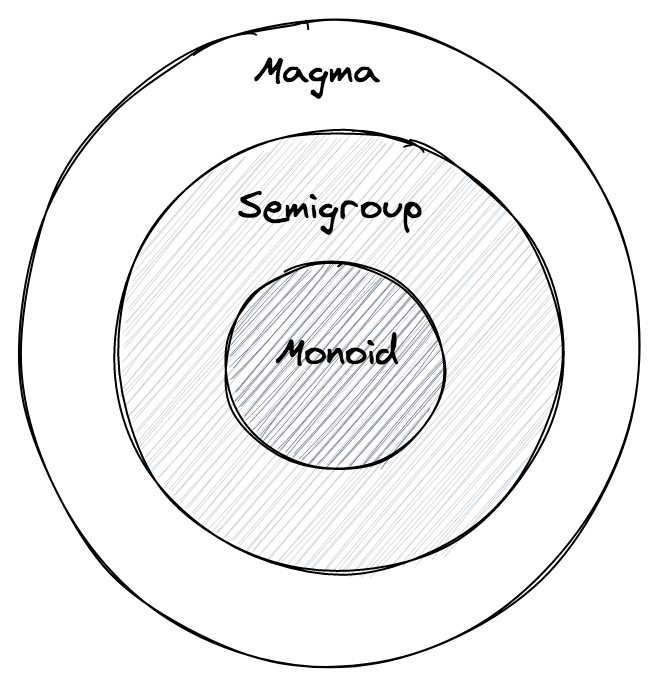
We have seen how each semigroup was a magma, but not every magma was a semigroup. In the same way, each monoid is a semigroup, but not every semigroup is a monoid.

Example

Let's consider the following example:

import { pipe } from 'fp-ts/function'
import { intercalate } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))

console.log(S.Semigroup.concat('a', 'b')) // => 'ab'
console.log(SemigroupIntercalate.concat('a', 'b')) // => 'a|b'
console.log(SemigroupIntercalate.concat('a', '')) // => 'a|'

Note how for this Semigroup there's no such empty value of type string such as concat(a, empty) = a.

And now one final, slightly more "exotic" example, involving functions:

Example

An endomorphism is a function whose input and output type is the same:

type Endomorphism<A> = (a: A) => A

Given a type A, all endomorphisms defined on A are a monoid, such as:

• the concat operation is the usual function composition
• the unit, our empty value is the identity function

import { Endomorphism, flow, identity } from 'fp-ts/function'
import { Monoid } from 'fp-ts/Monoid'

export const getEndomorphismMonoid = <A>(): Monoid<Endomorphism<A>> => ({
  concat: flow,
  empty: identity
})

Note: The identity function has one, and only one possible implementation:

const identity = (a: A) => a

Whatever value we pass in input, it gives us the same value in output.

The concatAll function

One great property of monoids, compared to semigrops, is that the concatenation of multiple elements becomes even easier: it is not necessary anymore to provide an initial value.

import { concatAll } from 'fp-ts/Monoid'
import * as S from 'fp-ts/string'
import * as N from 'fp-ts/number'
import * as B from 'fp-ts/boolean'

console.log(concatAll(N.MonoidSum)([1, 2, 3, 4])) // => 10
console.log(concatAll(N.MonoidProduct)([1, 2, 3, 4])) // => 24
console.log(concatAll(S.Monoid)(['a', 'b', 'c'])) // => 'abc'
console.log(concatAll(B.MonoidAll)([true, false, true])) // => false
console.log(concatAll(B.MonoidAny)([true, false, true])) // => true

Quiz. Why is the initial value not needed anymore?

Product monoid

As we have already seen with semigroups, it is possible to define a monoid instance for a struct if we are able to define a monoid instance for each of its fields.

Example

import { Monoid, struct } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'

type Point = {
  readonly x: number
  readonly y: number
}

const Monoid: Monoid<Point> = struct({
  x: N.MonoidSum,
  y: N.MonoidSum
})

Note. There is a combinator similar to struct that works with tuples: tuple.

import { Monoid, tuple } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'

type Point = readonly [number, number]

const Monoid: Monoid<Point> = tuple(N.MonoidSum, N.MonoidSum)

Quiz. Is it possible to define a "free monoid" for a generic type A?

Demo (implementing a system to draw geoetric shapes on canvas)

03_shapes.ts